纯干货（）这就是立项原文，仅供参考，严禁原文再次发表或使用

项目简介

时域天文学主要研究天体的各种性质如何随时间变化，这可能是由于天体本征性质发生改变，也可能源自其运动。分属时域天文领域的变星是光度随时间（周期）变化的恒星，其作为天体物理学中的重要研究对象，可应用于银河系和附近星系的结构和运动学示踪，星系化学演化示踪，研究恒星可变性也有助于我们理解恒星本身的演化和物理特性等，是许多领域的主要科学驱动力。随着科技进步，观测手段不断改进，在海量天体观测数据中对变源进行证认，仅凭目视分类法在时间和人力上都难以实现。藉由计算机领域的机器学习方法，对变星及其它变源（如系外行星凌星、活动星系核AGN等）进行特征提取并分类，是时域天文学前沿领域的重要课题，也是本项目的主要研究方向。本项目研究成果可应用于当前及未来时域巡天观测项目（如司天等）。

研究综述

至少归纳总结5个同类课题的研究观点/结论

1. 光变曲线特征提取

   提取变星周期使用的方法为周期图，其核心思想为傅里叶变换，该方法同样适用于恒星星震信号、恒星自转信号的搜索。傅立叶变换是一种线性的积分变换，常用 来对信号进行时域到频域的处理，对光变数据的傅立叶分析就是一个从时域到频域的 变换．我们使用Lom-Scargle(L-S)周期图和Box Least Squares(BLS)周期图法，其中L-S周期图(Lomb-Scargle)算法能很好地检测和提 取不均匀采样时域中的周期性，并且在不同学科的时序分析中得到了广泛的应用，它允许对不均匀采样的数据进行傅里叶变换，从而可以直观地表征光变周期.在L-S算法中， 只有时间序列中t时刻为实测值时才对光变数据进行处理，如果序列yi(ti)由N个数据点构成，将角频率w>0位变量的L-S周期频谱用Px来表示，则根据Lomb和Scargle的工作，可以按下式对Px进行计算：

   

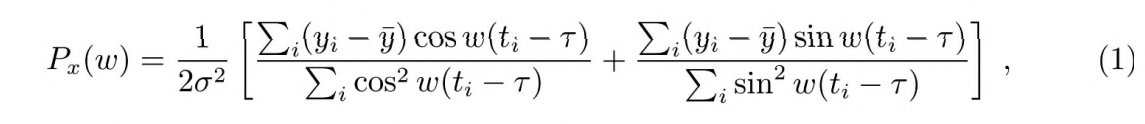
   另一种方法是BLS周期图，当凌星过程占行星轨道周期的比例较小时，BLS周期图 更加精确，对较长周期行星凌星使用BLS周期图法，利用该方法相较于L-S周期图可以找到更准确的信号峰值。（唐延柯、盖宁et al,2021,TESS空间卫星单扇区变星的周期性研究）

2. K-Means聚类方法属于迭代算法，根据分类个数随机生成相应个数的聚类中心，然后进入内循环，不断重复簇分配和移动聚类中心两个步骤，原则上靠近哪个聚类中心就被分为哪一类，可以用颜色区分标记，再移动聚类中心置属于该聚类中心的特征类的均值中心，簇分配和移动聚类中心的过程就是在不断地最小化代价函数。(Zafiirah Hosenie,Robert Lyon, Benjamin Stappers, Arrykrishna Mootoovaloo, 2019, Comparing Multi-class, Binary and Hierarchical Machine Learning Classification schemes for variable stars)

3. 主成分分析方法（PCA）主要是通过数据压缩，或者说降维的方法来加速学习过程，通过数据可视化、均值归一化和特征规范化的方法使得均值为0，且数值在可比较的范围内，就此寻找低维平面，将数据投影使得数据到平面的距离的平方（投影误差）最短；独立成分分析方法（ICA）同样用于降维，但相较于PCA多了独立性。在不同样本重叠的时候，ICA的特征分离效果更显著，效率更高。(Suman Paul, Tanuka Chattopadhyay, 2022, Structural properties and classification of variable stars: A study through unsupervised machine learning techniques)

4. SOM算法将一个N维的数据集（由N个估计值或参数组成）还原成一个由mxn个单元组成的二维网格。这使得SOM成为可视化高维数据集中相关关系的有力工具。SOM优势在于，它不仅能够稳健地识别给定AGN数据集中的可变光曲线，而且也是研究多维空间中物理参数之间相关性的工具–例如AGN可变性与其宿主星系属性之间的联系。(Faisst et al, 2019, How to Find Variable Active Galactic Nuclei with Machine Learning)

5. 关于 SOM 的训练，其输入参数有两个，分别是影响 Kohonen 层中像素调整速率的初始学习率$\alpha_0$和影响组大小的初始学习半径$\sigma_0$。对于一系列迭代，将每个输入的相位曲线与 Kohonen 层进行比较，并最小化像素元素和相位曲线之间的差异，找到层中的最佳匹配像素，然后按照以下表达式（Kohonen 层为二维的情况）更新每个像素：

   

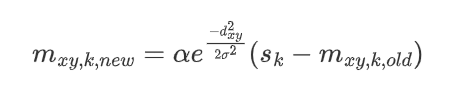
   其中：

   • $m_{xy,k,new}$是相位曲线中元素$k$、坐标$x,y$处的像素值。
   • $d_{xy}$是该层中这个像素与最佳匹配像素的欧几里得距离。
   • $s_k$是所考虑的相位曲线的第$k$个元素。

     对每个相位曲线执行该操作后，$\alpha$和$\sigma$将按照以下公式更新：

   

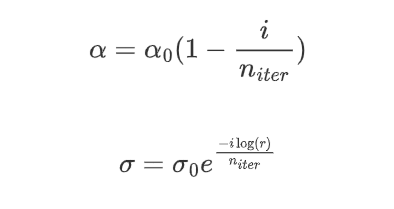
   其中：

   • i 是当前迭代轮数。
   • r 是 Kohonen 层最大维度的大小。
   • $n_{iter}$是进行迭代的次数。

6. Repeating this project with a dataset that is larger, more balanced between categories, and has a lower proportion of edge cases, is recommended.（T. N. Stenborg，2020，Machine Learning Classification of Candidate Variable Stars in Python）

7. Image classification was automated here via multinomial logistic regression. The six classes used were: pulsator, rotator, EA/EB type, EW type, unknown and junk. （T. N. Stenborg，2020，Machine Learning Classification of Candidate Variable Stars in Python）

参考文献

1. Zafiirah Hosenie,Robert Lyon, Benjamin Stappers, Arrykrishna Mootoovaloo, 2019, Comparing Multi-class, Binary and Hierarchical Machine Learning Classification schemes for variable stars
2. Suman Paul, Tanuka Chattopadhyay, 2022, Structural properties and classification of variable stars: A study through unsupervised machine learning techniques
3. Xiaodian Chen1 , Shu Wang et al. 2020, The Zwicky Transient Facility Catalog of Periodic Variable Stars
4. T. N. Stenborg, 2020, Machine Learning Classification of Candidate Variable Stars in Python
5. Andreas L. Faisst, Abhishek Prakash, Peter L. Capak, and Bomee Lee, 2019, How to Find Variable Active Galactic Nuclei with Machine Learning
6. Joseph W. Richards, Dan L. Starr et al. 2011, ON MACHINE-LEARNED CLASSIFICATION OF VARIABLE STARS WITH SPARSE AND NOISY TIME-SERIES DATA
7. D. J. Armstrong, J. Kirk, K. W. F. Lam et al. 2016, K2 variable catalogue – II. Machine learning classification of variable stars and eclipsing binaries in K2 fields 0–4
8. Ilya N. Pashchenko, Kirill V. Sokolovsky, and Panagiotis Gavras, 2017, Machine learning search for variable stars
9. Jan van Roestel, Dmitry A. Duev, Ashish A. Mahabal et al. 2021, The ZTF Source Classification Project. I. Methods and Infrastructure
10. 唐延柯,盖宁 et al. 2021, TESS空间卫星单扇区变星的周期性研究
11. 王瑞, 2021, 深度学习在LAMOST光谱恒星参数测量中的应用

研究方案

研究内容

本项目计划首先对变星数据进行数据获取和预处理，提取光变曲线主要特征，后使用DNN和SOM两种算法对变星分类，然后根据训练结果和测试结果进行超参数调优和优化器调整，预期得出准确率较高的分类结果。后期计划尝试其他无监督学习算法，与主要的两种算法进行对比；并尝试添加变星除光变曲线之外的其他观测特征进行Meta Learning训练。

研究方法

1. 收集整理相关变源时序测光数据，处理分析测光数据，提取数据光变特征信息；
2. 将获取的测光数据进行分类，处理可能出现的不平衡的数据情况，组成训练集和测试集；
3. 搭建深度神经网络DNN和自组织映射SOM 算法，对变源进行证认、分类测试；
4. 分析证认分类效果，优化改进算法，研究相关优化器并对超参数等进行调整，提高算法分类的准确率；
5. 测试其他相关算法，并与主要的两种算法效果进行对比，得出结论；
6. 综合以上研究，给出适用于大样本变源自动证认与分类的普适性算法、程序。

进度安排

计划将研究过程分为三个阶段：

1. 项目前期：学习时域天文学、机器学习相关内容，做好知识储备；获取相关天文观测数据，掌握从光变曲线中分析提取特征、消除噪声的方法，并进行数据集的初步处理；查阅相关文献，学习文章所涉及ML分类算法，进行迁移应用；
2. 项目中期：确定训练集和测试集，并对可能存在数据不平衡情况进行处理；结合所学构建ML主体算法，进行超参数调优，优化器调试等，最终得到准确率较高的分类结果；进行其他ML算法的尝试，并与主体算法相对比，比较二者（或多者）的优劣；尝试添加变星除光变曲线之外的其他观测特征进行训练。
3. 项目后期：完成上述工作后，对所得结果进行分析，并最终以论文的形式阐述研究结果，进行发表。

重点难点

1. 不同于常规的机器学习项目，有关时域天文领域的数据具有其自身特点，难以将现有的、发展完备的算法直接应用到相关数据分析当中；
2. 观测数据量大，难以直接使用原始光变曲线进行分析，可能需要依据变星特征提取重要光变信息作处理；
3. 天文观测数据易受天气条件限制，同一类数据受不同噪声的影响呈现效果有所不同，易造成分类准确率下降；
4. 对于某些变星，仅凭借光变曲线这一特征不足以对其进行正确分类，可能需要其他相关数据的配合；
5. 目前的观测数据中，脉动变星、食变双星的观测数据量较多，而相比之下喷发变星、激变或爆发变星观测数据量较少，易导致数据集产生不平衡的问题，从而可能对分类的精确率和召回率产生影响；
6. 特殊地，某些变星根据天文学的分类方式可以同时分属两个系统，对此类数据的分析处理存在一定困难。

创新之处

1. 天文学传统的目视分类法难以满足目前迅速增长的观测数据量的支持，使用机器学习进行分类能大量减少目前目视证认变星的负担，代替人类完成分类工作；
2. 机器学习在时域天文学的应用刚刚起步，发展前景广阔，本项目发掘有效的变星分类手段，为时域天文学领域发展做出贡献；
3. 项目并不局限于一种分类方式，而是有监督、无监督学习均有涉及，通过多种算法的尝试得出最终结论。
4. 本项目研究成果可应用于当前及未来时域巡天观测项目（如司天等）。

研究基础

本项目有关的研究工作积累或相关课程经验积累

1. 项目成员对天文学有浓厚兴趣，已学习天文学新概论、基础天文学等课程内容，并阅读变星相关文献进行学习；
2. 目前已有大量变源观测数据可供研究使用，如K2、TESS、ZTF等观测项目；
3. 机器学习方面计算机专业成员已有相关课程（机器学习、深度学习等）提供理论支持，并拓展课外相关知识，主动学习；
4. 指导老师认真负责，在天文学领域造诣颇深，为项目组成员提供切实有效课题知识指导。

指导老师意见

本项目针对当前天文学与天体物理学研究的热门前沿领域之一的“时域天文学”，利用机器学习、人工智能AI等创新方法手段对变源进行自动证认与分类研究分析，可帮助解决大数据背景下的重要科学问题，也可进一步促进机器学习方法在天文学中应用，加强天文物理与计算机信息技术、数学统计等领域的交叉融合，此外其研究成果可应用于当前及未来时域巡天观测项目（如司天等），具有重要意义。强烈建议项目立项！